где tH.n,<c - температура необогреваемой поверхности за время т, °С; t„.n(T.-At> - температура необогреваемой поверхности за время (т-Ат), °С; t,s Ax. х - температура в начале последнего слоя за время т, °С; t0 - начальная температура, °С. В уравнении (4.36) коэффициенты теплопроводности Kt и теплоемкости ct определяются при средней температуре последнего слоя за время (т-Ат), а коэффициент теплопередачи ан.п по формуле (4.11) при температуре необогреваемой поверхности за время (т-Ат).

Пример. Определить предел огнестойкости сплошной железобетонной стены толщиной 6 = 0,12 м по признаку прогрева необогреваемой поверхности до температуры, превышающей первоначальную на 160°С. Характеристики бетона: заполнитель - крупный гранитный щебень; объемная масса в сухом состоянии рс = 2330 кг/м3; эксплуатационная весовая влажность Рв = 2,0%.

Решение. 1. Определяем исходные данные:

теплофизические характеристики бетона определяем по формулам из табл. 4.1 при температуре 250°С:

ХСР = 1,2-0,0035t= 1,2-0,0035-250= 1,11 Вт/(м-°С);

cctP = 0,71 +0,00084t = 0,71 +0,00084• 250 = 0,92 кДж/(кг-°С);

а = U1 ..

°Р (ccf +0,05Рв)рс (0,92+0,05-2)2330

=0,000467 (Вт• м2) /кДж=0,00168 м2/ч.

2. Разбиваем сечение конструкции на четыре слоя, с толщиной каждого Дх = 0,03 м, и определяем интервал времени:

Дх2 0,0009

Дт=-- = -!-=0,268 ч.

2апр 2-0,00168

3. По уравнению (4.22) определяем температуру обогреваемой поверхности. Значение коэффициента к=0,63 находим из табл. 4.4.

При т=0,268 ч:

/ 0 63 \

t = 1250- (1250-20) erf f- =507°С.

\ 2 V 0,268 )

0,63

где А=- =0,6; erf=0,604 (прил. 1).

2 V 0,268

При т=0,536 ч:

ton=1250- (1250-20)erf

/ 0,63 \ \ 2 V 0,536 )

Данные по температуре обогреваемой поверхности заносим в графу табл. 4.5.

Таблица 4.5

4. По формуле (4.35) определяем значения температуры на границах слоев.

5. Определяем температуру необогреваемой поверхности по уравнению (4.36). По данным табл. 4.5 при T = 0,268-f-0,804 ч уравнение (4.36) принимает следующий вид:

*н.п,Т =tH.n(T. -Д X) =20°С.

При т1,07 ч необходимо для каждого периода времени вычислять kv ct

И «я

При т=1,07 ч: t = 20+20 =20°С; op 2

A,t = 1,2-0,00035-20=1,193 Вт/ (м • °С); С(. == 0,71+0,00084 • 20 = 0,727 кДж/ (кг• °С);

«н.п = ««+«., = 1-5 Y tH.n-20 +5,67ен.д

!±У 73,7 100 /

t„.»-20

= 0;

= 20+ , 2.0,268-1,193(81-20) = 2330-0,0009-0,727

3 з. 1851

Полученное значение температуры заносим в последнюю графу табл. 4.5-В этом случае V~Ax>t=M = ~~~~~~~==116°С.

При т= 1,34 ч: *ср= 81"46 =63,5°С;

\ = 1,2-0,00035 • 63,5 = 1,178 Вт/ (м • °С); с, = 0,71 +0,00084 63,5 = 0,763 кДж/ (кг • °С);

/ 46+273 V

, - - 73,7

\ 100

«вя = 1,5 3]/46--20>567Ч064-0,00045-46) v

46 - 20

= 8,3 Вт/(м2-°С),

где 8В п = 0,64 - 0,00045tH п (по табл. 4.3);

1,178(116-46) -8,3 • 0,03 (46-20) .. W,34 =46+0,256 ----------~

*(6-Лх)- = 1,61 = 272+71 « 172°С и т. д. 2

При т = 2,41 ч tHn=185°C. Интерполяцией находим:

ПЛ=2,4 ч. Ф

При двухмерном температурном поле на сечение конструкции накладывается сетка с размерами ячейки Ау. Расчетный интервал времени Ат находят по формуле

Дт=- Лу2 . (4-37)

4аи.р

Температуру в узловых точках сетки через интервал времени Ат находят как среднее арифметическое значений температур в соседних узлах. Так, для узла 5 (рис. 4.6) формула имеет следующий вид:

*2(Т-А ~> ~4( Т-А~> ~s< T-ATj +t6(T -АТ> gg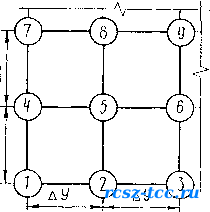

Рис. 4.6. Схема к определению температуры в узловых точках при двухмерном температурном поле

Во всех случаях задача решается применительно к граничным условиям 1-го рода. Если температура обогреваемой поверхности Не задана как функция времени, то ее определяют по эмпирическим (ррмулам.

4.3. Расчет температурных полей с помощью ЭВМ

Недостатком расчета температурных полей в конструкциях помощью аналитических зависимостей является его приближенность вследствие усреднения теплофизических характеристик ма-

fриалов конструкций и коэффициентов теплообмена их поверхно-ей с окружающей средой, а также невозможность получения рас-Итных формул для конструкций со сложной конфигурацией попе-

Йчного сечения, например, колонн и балок двутаврового сечения, етод Шмидта, хотя и применим для расчета температурного поля поперечном сечении конструкций любой конфигурации, является Цкже приближенным из-за усреднения теплофизических характе-рстик материалов.

Отмеченные недостатки устраняются при использовании машин-§Sro расчета, который дает возможность определить температурные

?ЛЯ при внешней и внутренней нелинейности теплопередачи прак-Чески в любых конструкциях при любых граничных условиях. Машинный расчет основан на использовании уравнений Фурье. Щиболее простым для понимания физической сущности теплопере-

С*Ш разностным методом является метод элементарных тепловых (Лансов А. П. Ваничева. Применительно к расчету огнестойкости

строительных конструкций этот метод был усовершенствован путем учета в расчетных уравнениях влияния начальной влажности мате риалов, массы и размеров арматуры и стальных элементов на тем пературное поле в сечении конструкций с применением металла.

Количество и вид уравнений алгоритма расчета зависит от многих факторов: сечения, конструктивного исполнения, способов обо грева конструкций, начальных и граничных условий и т. д.

Принципы составления уравнений алгоритма расчета на ЭВМ рассмотрим на примере применения его для случая плоской сплош ной конструкции.

Общую толщину конструкции разбивают на ряд элементарных слоев Дх (рис. 4.7). Затем составляют уравнения теплового балан са для каждого расчетного слоя, из которых получают формулы для определения температуры в этих слоях через расчетный интер вал времени Ат. Расчетные температурные точки располагаются на наружных поверхностях конструкции и границах элементарных слоев.

При составлении расчетных уравнений принимают следующие предпосылки и допущения: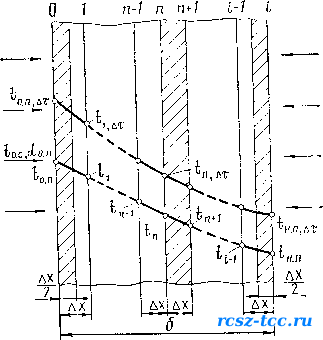

Рис. 4.7. Схема к расчету температур в ограждающей конструкции с помощью ЭВиМ.

передача тепла за счет влагопереноса отсутствует; свободная 1Лага испаряется в слоях последовательно по мере прогрева их до Температуры кипения воды 100°С; образовавшийся пар удаляется 1 сторону обогреваемой поверхности, т. е. навстречу тепловому потоку;

тепло, поступающее в элементарный слой, расходуется на испарение свободной влаги в порах материала и на увеличение теплосодержания слоя;

распределение температур по толщине элементарного слоя принимается прямолинейным;

изменение теплофизических свойств материала при прогреве Конструкции учитывается введением в уравнения формул вида:

>4 = A + Bt. (4.39)

сС + Дх. (4.40)

Коэффициенты теплопроводности Kt и теплоемкости ct дол лены ©пределяться при средней температуре слоя. Вместе с тем анализ Начений опытных коэффициентов А, В, С, и Д (см. табл. 4.1 и 4.2) Показывает, что некоторое отклонение температуры от истинной Не влияет на результаты расчета, так как значения коэффициентов В и Д в среднем на три порядка меньше значений А и С. Поэтому, С целью упрощения расчета, Xt и ct определяют при известных значениях температуры на границах элементарных слоев.

Расчетную формулу для определения температуры обогреваемой Поверхности т.0.п,д- получают из уравнения теплового баланса полу-СЛоя Ах/2 с площадью тепловоспринимающей поверхности, равной I м2:

Oo.n(to.o-to.«)AT---ft„.„- U + tl )ат =

Ах у 2 у

= с,рс-- (t0.„,A т -t0.n)+QB, (4.41)

ГДе t0.c - температура окружающей среды, °С; QB - расход тепла на испарение свободной влаги в порах материала конструкции, кДж.

С учетом уравнений (4.39) и(4.40) имеем:

2Ат / д , „ t0.„ + ti \( х t„.n + t, \

.*."(*<,.-1о.=)Дт--=-- А + В °-д м t

Ах \ 2 Д 2

= Рс -- (С+Д10.п)(т0.п,дт - t„.n)+QB. (4.42)